Unveiling the Power of Karnaugh Maps: Simplifying Boolean Expressions with Product of Sums
Related Articles: Unveiling the Power of Karnaugh Maps: Simplifying Boolean Expressions with Product of Sums
Introduction
With great pleasure, we will explore the intriguing topic related to Unveiling the Power of Karnaugh Maps: Simplifying Boolean Expressions with Product of Sums. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
Unveiling the Power of Karnaugh Maps: Simplifying Boolean Expressions with Product of Sums
In the realm of digital logic design, simplifying Boolean expressions is paramount. It optimizes circuit implementations, reduces component count, and enhances performance. One powerful tool for achieving this simplification is the Karnaugh map (K-map), a graphical representation of Boolean functions that facilitates the identification of minimal sum-of-products (SOP) or product-of-sums (POS) expressions.
This exploration delves into the intricacies of K-maps and their application in deriving product-of-sums (POS) expressions, highlighting the benefits and intricacies of this approach.
Understanding the Fundamentals of Karnaugh Maps
Karnaugh maps, named after Maurice Karnaugh, are a visual aid for simplifying Boolean expressions. They represent the truth table of a Boolean function in a grid format, where each cell corresponds to a unique combination of input variables. The arrangement of cells is crucial, ensuring that adjacent cells differ by only one variable. This strategic arrangement facilitates the identification of groups of adjacent cells representing minterms or maxterms, enabling the simplification process.
The Essence of Product of Sums (POS)
Product of sums (POS) is a form of Boolean expression where individual sum terms (OR operations) are combined using AND operations. It represents a logical function where the output is true only when all the sum terms are true. This contrasts with the sum of products (SOP) form, where individual product terms (AND operations) are combined using OR operations.
Constructing Karnaugh Maps for POS Expressions
To derive a POS expression using a K-map, the focus shifts from identifying minterms (corresponding to "1" entries in the truth table) to identifying maxterms (corresponding to "0" entries). Maxterms represent the conditions under which the function is false.
-
Create the K-map: The size of the K-map is determined by the number of input variables. For example, a 4-variable function requires a 2×4 K-map.
-
Populate the K-map: Each cell in the K-map corresponds to a unique combination of input variables. Enter a "0" in the cells representing the maxterms (combinations where the function is false) and a "1" in the cells representing the minterms (combinations where the function is true).
-
Identify the groups of "0" entries: The goal is to find the largest possible groups of adjacent "0" entries, including wrapping around the edges of the K-map. These groups represent the maxterms that can be combined to form the POS expression.
-
Write the POS expression: Each group of "0" entries corresponds to a sum term. The variables within the group are negated (inverted), and the sum term is combined with other sum terms using AND operations.
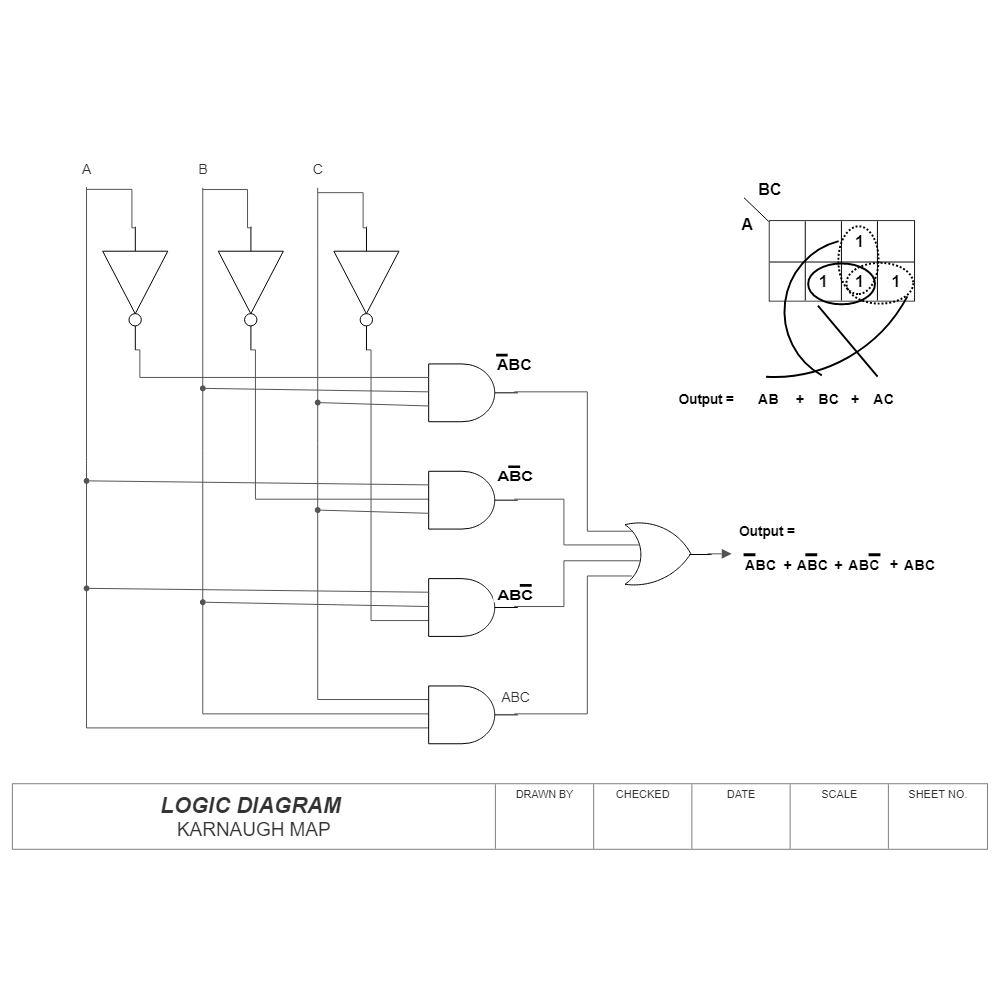
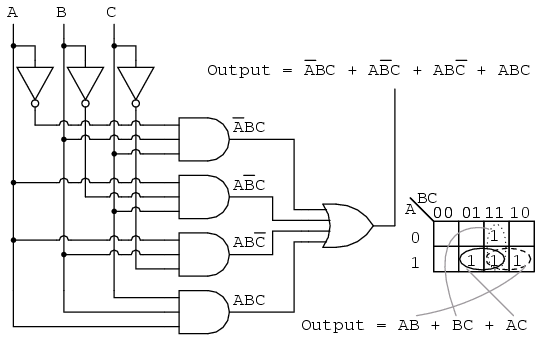
Illustrative Example: Deriving a POS Expression
Consider a Boolean function with three input variables, A, B, and C, and its truth table:
| A | B | C | F |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
To derive the POS expression using a K-map:
-
Create a 2×4 K-map: The rows represent the combinations of A and B, and the columns represent the combinations of C.
-
Populate the K-map: Enter "0" in the cells corresponding to the maxterms (rows 3, 6, 7, and 8) and "1" in the cells corresponding to the minterms (rows 1, 2, 4, and 5).
-
Identify groups of "0" entries: There are three groups of "0" entries:
- Group 1: Cells (0,1,0) and (1,1,0) (representing maxterm A’B’C and maxterm ABC)
- Group 2: Cells (1,0,1) and (1,1,1) (representing maxterm A’BC and maxterm ABC)
- Group 3: Cells (0,1,0) and (0,1,1) (representing maxterm AB’C and maxterm ABC)
-
Write the POS expression: The POS expression is obtained by combining the sum terms corresponding to each group:
(A’B’C + ABC) (A’BC + ABC) (AB’C + ABC)
This expression can be further simplified by applying Boolean algebra identities, resulting in:
(A'C + BC) * (A' + B)Advantages of Using POS Expressions
Deriving POS expressions using K-maps offers several advantages:
-
Simplicity: K-maps provide a visual representation of Boolean functions, making it easier to identify groups of maxterms and simplify the expression.
-
Efficiency: Compared to algebraic manipulation, K-maps offer a faster and more intuitive approach to simplification.
-
Minimization: POS expressions obtained through K-maps are often minimal, meaning they use the fewest possible literals (variables) and operations, leading to simpler and more efficient circuits.
-
Dual Representation: The POS form is the dual of the SOP form, meaning that it provides an alternative representation of the same Boolean function. This dual representation can be beneficial in certain applications where one form might be more advantageous than the other.
Common Applications of POS Expressions
POS expressions find practical applications in various areas of digital logic design:
-
Circuit Design: POS expressions are used to design logic circuits that implement Boolean functions. The POS form can be implemented using AND gates for the sum terms and OR gates for the product terms.
-
Logic Optimization: POS expressions are essential for optimizing logic circuits, reducing the number of gates and connections, and improving circuit performance.
-
Verification and Testing: POS expressions can be used to verify the correctness of logic circuits and to generate test vectors for identifying potential faults.
Frequently Asked Questions (FAQs)
Q: What are the limitations of K-maps?
A: K-maps are effective for simplifying Boolean functions with up to six variables. However, for functions with more variables, their complexity increases significantly, making them less practical.
Q: When should I use SOP vs. POS expressions?
A: The choice between SOP and POS depends on the specific application and the desired circuit implementation. In general, SOP expressions are more commonly used due to their ease of implementation. However, POS expressions can be advantageous when minimizing the number of gates required for a circuit or when dealing with certain types of logic functions.
Q: Can I use K-maps for functions with don’t care conditions?
A: Yes, K-maps can be used to simplify functions with don’t care conditions. Don’t care conditions represent input combinations that are not relevant to the function’s output. They can be assigned either "0" or "1" in the K-map, allowing for further simplification.
Tips for Effective K-Map Use
-
Understand the K-map structure: Familiarize yourself with the arrangement of cells and the relationship between adjacent cells.
-
Identify the maxterms: Focus on the "0" entries in the K-map, as they represent the maxterms.
-
Form the largest possible groups: Aim to create groups of "0" entries that are as large as possible, covering as many adjacent cells as possible.
-
Consider wrapping around: Remember that the K-map wraps around at the edges, so groups can extend across the boundaries.
-
Simplify the POS expression: Use Boolean algebra identities to simplify the POS expression obtained from the K-map.
Conclusion
Karnaugh maps provide a powerful and intuitive method for simplifying Boolean expressions, enabling the derivation of minimal product-of-sums (POS) expressions. By understanding the principles of K-maps and their application in identifying maxterms, one can effectively optimize logic circuits, reducing component count and improving performance. The POS form, while less commonly used than the SOP form, offers a valuable alternative representation of Boolean functions, providing flexibility and efficiency in certain design scenarios. Mastering the art of K-maps empowers digital logic designers to create efficient and robust systems, contributing to the advancement of digital technologies.




Closure
Thus, we hope this article has provided valuable insights into Unveiling the Power of Karnaugh Maps: Simplifying Boolean Expressions with Product of Sums. We thank you for taking the time to read this article. See you in our next article!
