Unraveling The Power Of 4-Variable Karnaugh Maps: A Comprehensive Guide

Unraveling the Power of 4-Variable Karnaugh Maps: A Comprehensive Guide

Related Articles: Unraveling the Power of 4-Variable Karnaugh Maps: A Comprehensive Guide

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Unraveling the Power of 4-Variable Karnaugh Maps: A Comprehensive Guide. Let’s weave interesting information and offer fresh perspectives to the readers.

Unraveling the Power of 4-Variable Karnaugh Maps: A Comprehensive Guide

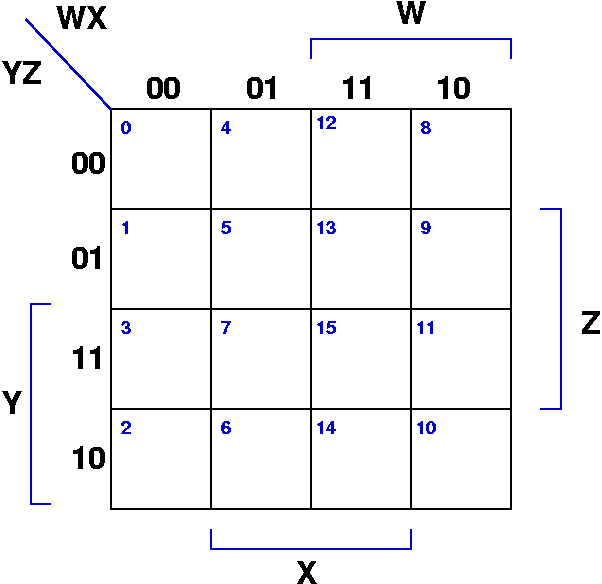
The realm of digital logic design hinges on the efficient manipulation of Boolean expressions. These expressions, representing complex logic circuits, can be simplified and optimized using various techniques. One such powerful tool is the Karnaugh map, a visual representation that facilitates the simplification of Boolean expressions with up to four variables. This guide delves into the intricacies of 4-variable Karnaugh maps, exploring their construction, application, and significance in digital circuit design.

Understanding the Fundamentals: A Visual Approach to Logic

A Karnaugh map, often called a K-map, is a graphical representation of a truth table. It organizes minterms (product terms) in a grid, where each cell corresponds to a unique combination of input variables. The arrangement of these cells follows a specific pattern, ensuring that adjacent cells differ by only one variable. This arrangement enables the identification of groups of minterms that can be combined to simplify the Boolean expression.

In the case of a 4-variable Karnaugh map, the grid consists of 16 cells, representing all possible combinations of four input variables. Each cell is labeled with a binary code representing the input values. The map is typically arranged as a 2×4 or 4×2 grid, where each row and column corresponds to a specific combination of two variables.

Constructing the 4-Variable Karnaugh Map: A Step-by-Step Guide

Building a 4-variable Karnaugh map involves the following steps:

1. Identify the input variables: Define the four input variables (A, B, C, D) that determine the output of the Boolean function.

2. Determine the output values: Create a truth table that lists all possible input combinations and the corresponding output values for the Boolean function.

3. Assign binary codes to input variables: Represent each input variable with a binary code (0 or 1) for each combination in the truth table.

4. Label the rows and columns: Label the rows and columns of the Karnaugh map with the binary codes of the input variables, ensuring that adjacent rows and columns differ by only one bit.

5. Fill the cells with output values: For each combination of input variables, place the corresponding output value (0 or 1) in the appropriate cell of the map.

Simplifying Boolean Expressions: The Art of Grouping Minterms

The true power of the Karnaugh map lies in its ability to simplify Boolean expressions by grouping adjacent minterms. This simplification process leverages the following key principles:

1. Adjacent cells: Adjacent cells in a Karnaugh map differ by only one variable. This implies that the minterms represented by these cells share all but one variable.

2. Grouping minterms: Minterms that are adjacent on the map can be combined into a single term by eliminating the variable that differs between them.

3. Grouping rules: Minterms can be grouped in powers of two (1, 2, 4, 8). Each group represents a simplified term in the final Boolean expression.

4. Covering all ‘1’ cells: All cells containing ‘1’ in the Karnaugh map must be covered by at least one group.

5. Minimum number of groups: The goal is to use the minimum number of groups possible to cover all ‘1’ cells, minimizing the complexity of the final Boolean expression.

Illustrative Example: Simplifying a Boolean Function

Consider the following Boolean function:

F(A, B, C, D) = Σm(0, 2, 4, 6, 8, 10, 12, 14)

This function represents a logic circuit with four input variables (A, B, C, D) and eight minterms (0, 2, 4, 6, 8, 10, 12, 14). To simplify this function using a Karnaugh map, we follow these steps:

1. Construct the Karnaugh map: Create a 4-variable Karnaugh map and fill the cells corresponding to the minterms listed in the function.

2. Identify adjacent groups: Group the ‘1’ cells on the map, ensuring that each group contains a power of two minterms.

3. Formulate the simplified expression: Write down the simplified Boolean expression based on the identified groups.

The resulting simplified expression for the given function is:

F(A, B, C, D) = A'D' + AC' + BD

This simplified expression represents a more efficient logic circuit compared to the original Boolean function.

Unveiling the Benefits: Why Karnaugh Maps Matter

The use of Karnaugh maps offers numerous advantages in digital logic design:

1. Simplified Boolean expressions: K-maps facilitate the simplification of complex Boolean expressions, reducing the number of logic gates required to implement the corresponding circuit.

2. Efficient circuit design: Minimizing the number of logic gates results in circuits with lower cost, reduced power consumption, and increased speed.

3. Visual representation: Karnaugh maps provide a visual representation of the Boolean function, making it easier to identify patterns and simplify the expression.

4. Improved readability: The graphical nature of K-maps makes them easier to understand and interpret compared to complex Boolean equations.

5. Systematic approach: The use of Karnaugh maps provides a systematic and organized approach to Boolean simplification, minimizing the risk of errors.

Frequently Asked Questions (FAQs) about 4-Variable Karnaugh Maps

Q1: What are the limitations of 4-variable Karnaugh maps?

A: While powerful for simplifying Boolean expressions with up to four variables, Karnaugh maps become increasingly complex for larger numbers of variables. For functions with five or more variables, alternative simplification techniques like the Quine-McCluskey method are more efficient.

Q2: Can Karnaugh maps handle functions with don’t care conditions?

A: Yes, Karnaugh maps can handle functions with don’t care conditions. These conditions represent input combinations where the output value is irrelevant. In the map, ‘X’ is used to denote don’t care conditions. During grouping, these cells can be included or excluded as needed to maximize simplification.

Q3: How can I visualize the simplified expression obtained from a Karnaugh map?

A: The simplified expression obtained from a Karnaugh map can be visualized using a logic diagram. Each term in the expression corresponds to a specific logic gate (AND, OR, NOT), and the connections between these gates represent the relationships between the variables.

Q4: Are there any software tools that can assist with Karnaugh map simplification?

A: Yes, several software tools are available that can assist with Karnaugh map simplification. These tools typically provide a graphical interface for creating and manipulating Karnaugh maps, as well as automated simplification algorithms.

Tips for Effective Karnaugh Map Simplification

1. Start with a clear understanding of the Boolean function: Before constructing the Karnaugh map, ensure a thorough understanding of the function’s input variables, output values, and truth table.

2. Use a systematic approach: Follow a structured approach when grouping minterms. Start with the largest possible groups, and gradually move to smaller groups as needed.

3. Double-check your work: After simplifying the expression, carefully verify that all ‘1’ cells in the map are covered and that the minimum number of groups is used.

4. Explore alternative groupings: Sometimes, multiple valid groupings can exist. Experiment with different groupings to ensure that you have found the most simplified expression.

5. Utilize software tools: Software tools can be helpful for creating, manipulating, and simplifying Karnaugh maps. However, it’s essential to understand the underlying principles of K-map simplification to interpret the results effectively.

Conclusion: Mastering the Art of Boolean Simplification

The 4-variable Karnaugh map is a powerful tool for simplifying Boolean expressions, leading to more efficient and optimized digital circuits. By understanding the principles of K-map construction, grouping, and simplification, designers can effectively minimize logic gates, reduce power consumption, and enhance circuit performance. While Karnaugh maps may have limitations for functions with a larger number of variables, they remain a valuable technique for simplifying Boolean expressions in a clear, visual, and systematic manner. Mastering the art of Karnaugh map simplification empowers digital logic designers to create efficient and reliable circuits for a wide range of applications.

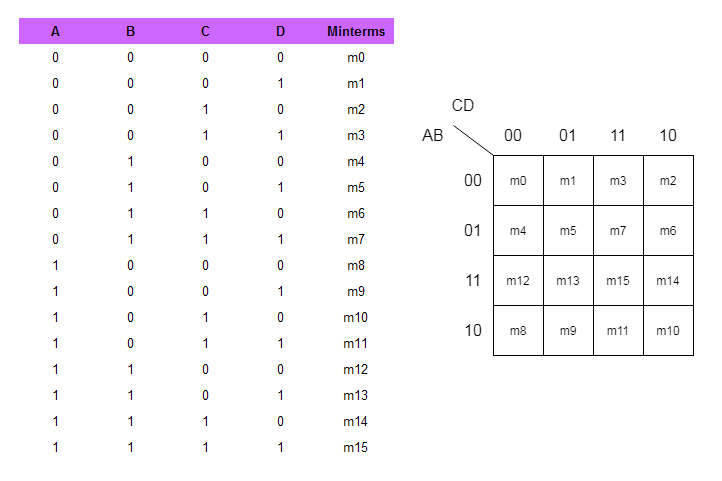
Closure

Thus, we hope this article has provided valuable insights into Unraveling the Power of 4-Variable Karnaugh Maps: A Comprehensive Guide. We hope you find this article informative and beneficial. See you in our next article!