Unlocking Mathematical Understanding: A Comprehensive Guide To Concept Mapping

Unlocking Mathematical Understanding: A Comprehensive Guide to Concept Mapping

Related Articles: Unlocking Mathematical Understanding: A Comprehensive Guide to Concept Mapping

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Unlocking Mathematical Understanding: A Comprehensive Guide to Concept Mapping. Let’s weave interesting information and offer fresh perspectives to the readers.

Unlocking Mathematical Understanding: A Comprehensive Guide to Concept Mapping

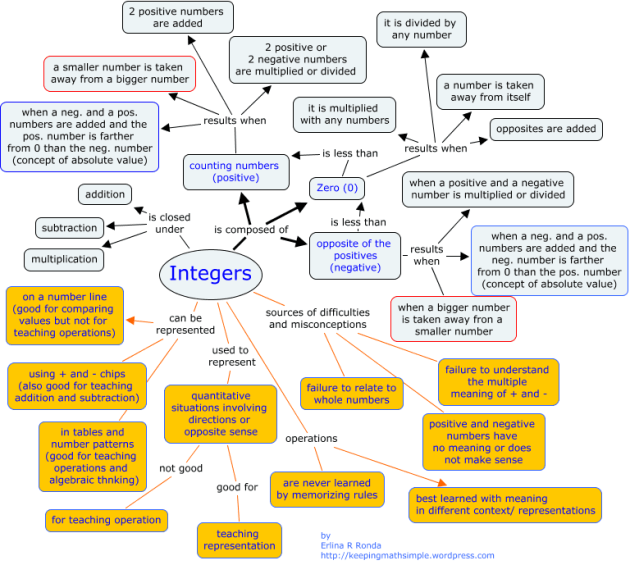
In the realm of mathematics, where abstract concepts and intricate relationships intertwine, a powerful tool emerges to illuminate the path to comprehension: concept mapping. This visual representation technique, akin to a cognitive roadmap, empowers learners to navigate the complexities of mathematical ideas and forge meaningful connections between them.

Understanding the Essence of Concept Mapping in Mathematics

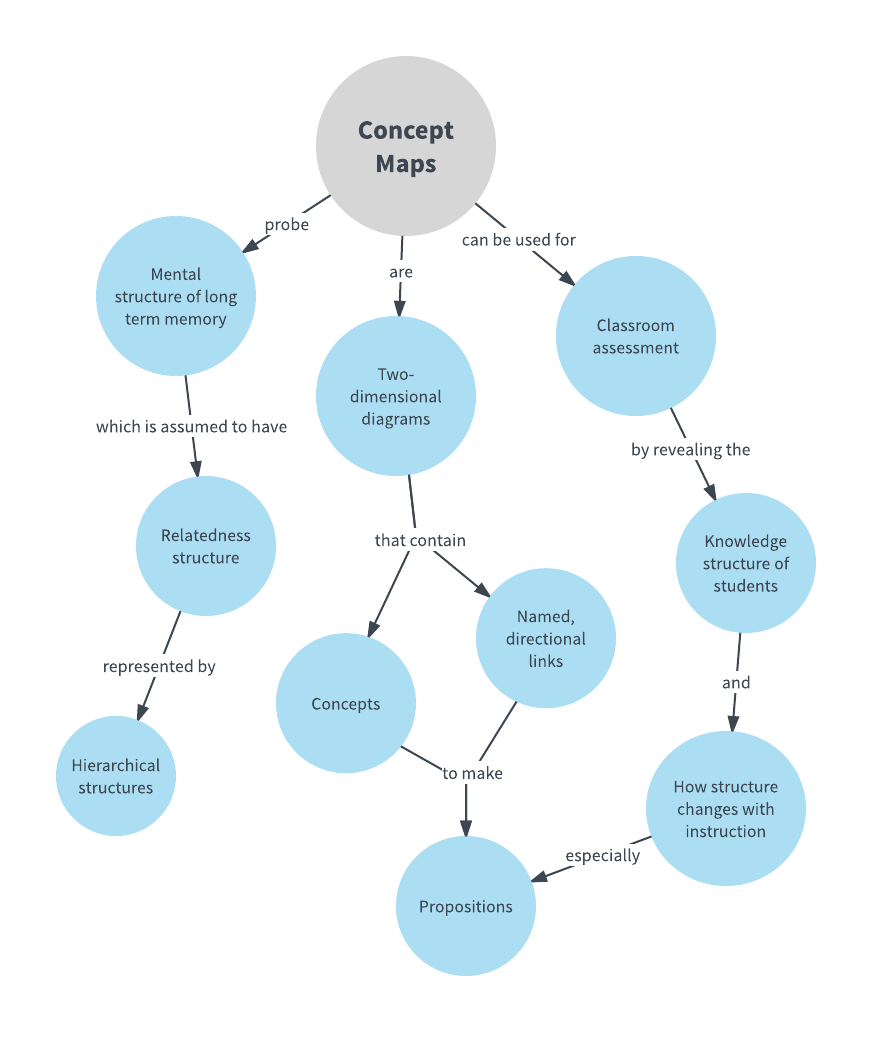
At its core, a concept map is a visual representation of knowledge, showcasing the interconnectedness of various mathematical concepts. It employs nodes, representing key ideas, and links, illustrating the relationships between them. These links can be hierarchical, showing the progression from fundamental principles to advanced concepts, or associative, highlighting the connections between seemingly disparate ideas.

The Advantages of Concept Mapping in Mathematics

The benefits of employing concept maps in mathematical learning are multifaceted and demonstrably impactful:

• Enhanced Comprehension: By visually organizing information, concept maps promote deeper understanding and retention. Learners can grasp the "big picture" of a mathematical topic, recognizing the interplay between different concepts and their underlying logic.
• Improved Memory Recall: The act of creating a concept map actively engages learners in the learning process, strengthening their memory recall. The visual structure aids in retrieving information and recalling the interconnectedness of ideas.
• Critical Thinking Development: Concept mapping encourages critical thinking by prompting learners to analyze, synthesize, and evaluate mathematical concepts. It fosters the ability to identify relationships, draw inferences, and make connections between different ideas.
• Problem-Solving Skills Enhancement: By exposing learners to the interconnectedness of mathematical concepts, concept maps facilitate problem-solving. They provide a framework for identifying relevant concepts, applying appropriate strategies, and arriving at logical solutions.
• Personalized Learning: Concept maps allow learners to personalize their learning experience. By tailoring the map to their individual needs and understanding, they can focus on areas requiring further exploration or clarification.

Building a Robust Concept Map in Mathematics

Constructing an effective concept map requires a systematic approach:

1. Identify the Central Concept: Begin by defining the core topic or concept you wish to map. This serves as the starting point for your map.
2. Brainstorm Related Concepts: Engage in a brainstorming session to identify key concepts related to the central concept. These can be subtopics, definitions, theorems, formulas, or any other relevant ideas.
3. Establish Hierarchical Relationships: Organize the brainstormed concepts hierarchically, placing the central concept at the top and arranging related concepts beneath it.
4. Draw Links and Label Relationships: Connect the nodes representing concepts with lines or arrows, labeling them with verbs or prepositions that describe the relationship between the concepts.
5. Refine and Iterate: Continuously refine your concept map by adding, removing, or re-arranging concepts and links as needed. This iterative process ensures a comprehensive and accurate representation of the subject matter.

Examples of Concept Maps in Mathematics

To illustrate the practical application of concept mapping in mathematics, let’s consider a few examples:

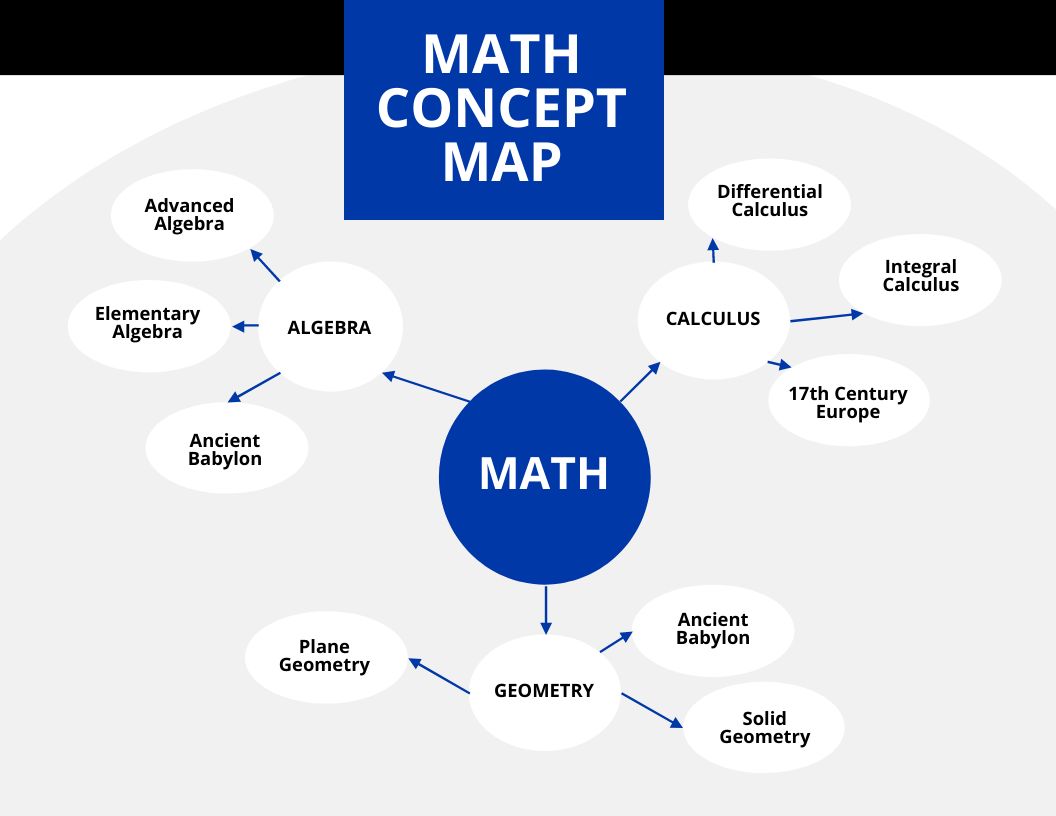
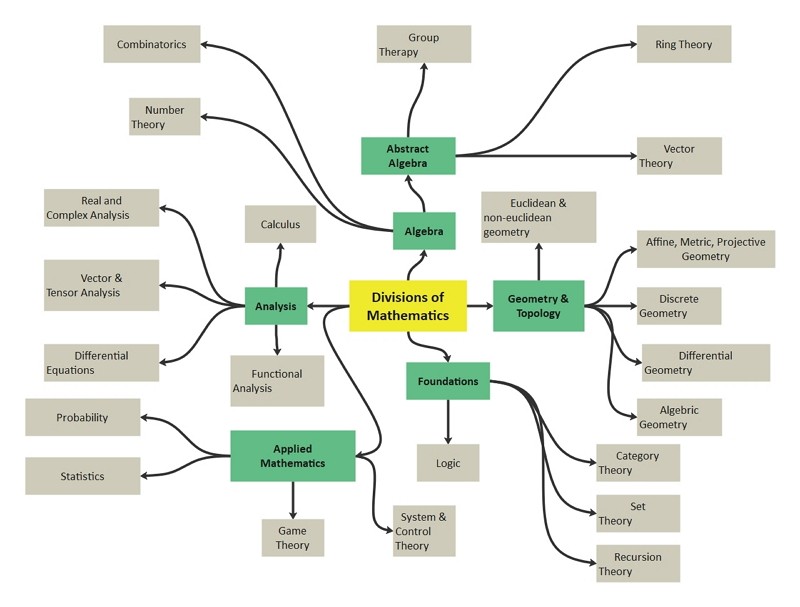
• Algebra: A concept map for algebra could encompass concepts like variables, expressions, equations, inequalities, and functions. The links would illustrate the relationships between these concepts, such as "variables are used in expressions," "equations express equality between expressions," and "functions represent relationships between variables."
• Geometry: A concept map for geometry might include concepts like points, lines, angles, shapes, and transformations. Links could demonstrate relationships such as "points define lines," "angles are formed by intersecting lines," and "transformations alter the position of shapes."
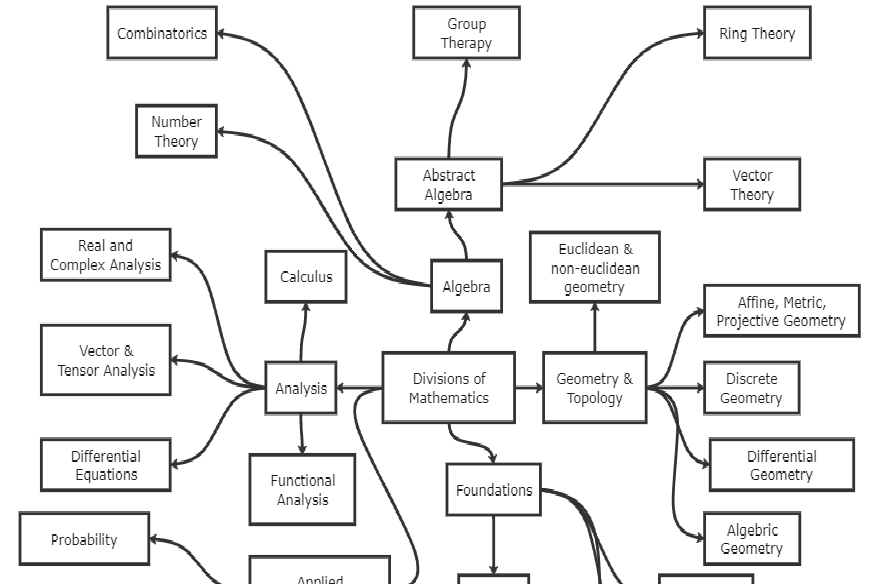
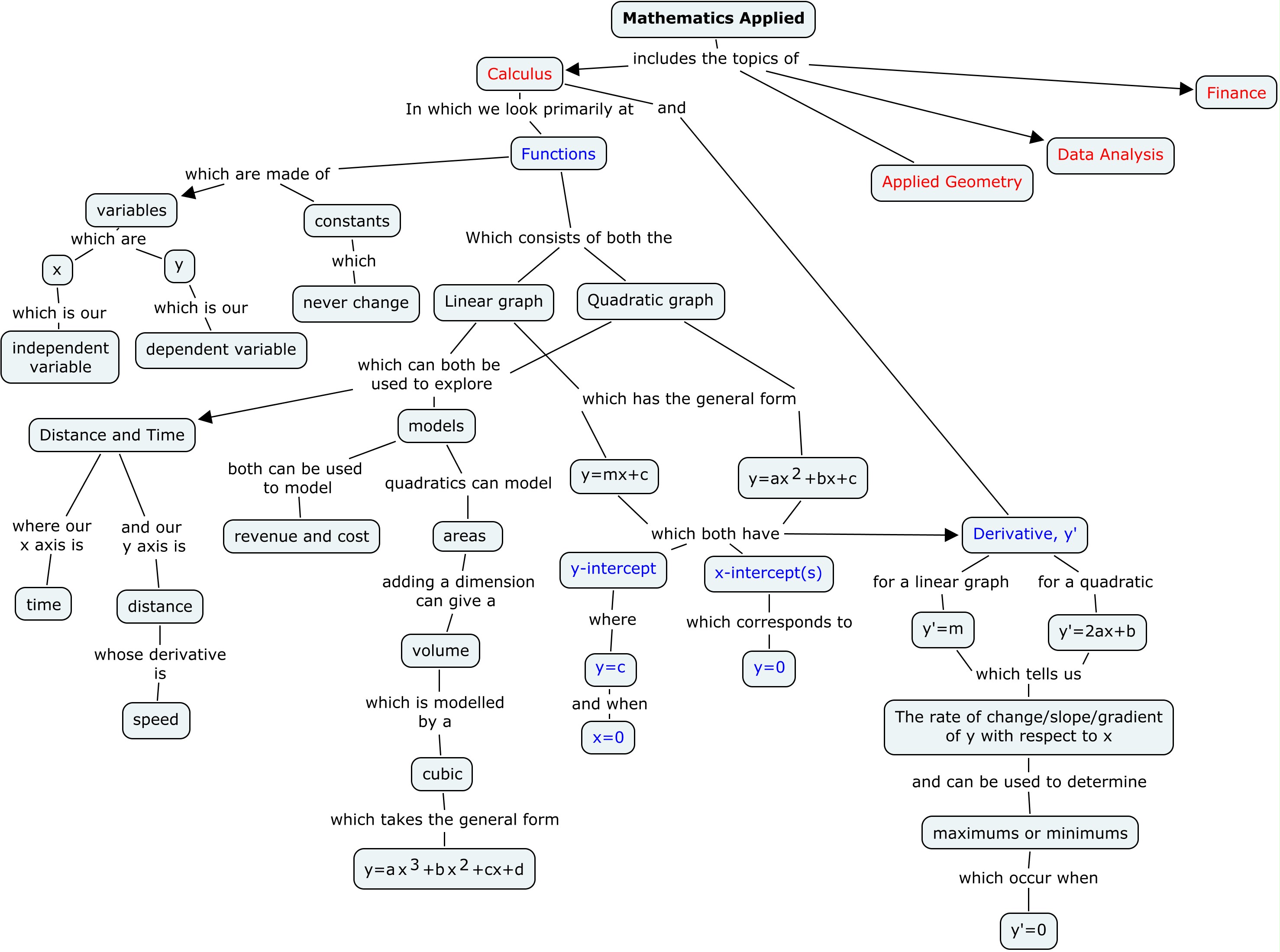
• Calculus: A concept map for calculus could focus on concepts like limits, derivatives, integrals, and applications of calculus. Links would highlight relationships such as "limits define the behavior of functions," "derivatives measure rates of change," and "integrals calculate areas under curves."

FAQs on Concept Mapping in Mathematics

Q: What is the best way to start creating a concept map in mathematics?

A: Begin by identifying the central concept you wish to map. Then, brainstorm related concepts and organize them hierarchically.

Q: How can I ensure my concept map is accurate and comprehensive?

A: Use reliable sources such as textbooks, articles, and online resources to verify the accuracy of your concepts and relationships. Continuously refine your map by adding, removing, or re-arranging concepts and links as needed.

Q: What are some common mistakes to avoid when creating concept maps?

A: Avoid overcrowding your map with too many concepts, using vague or ambiguous labels for links, and neglecting to review and refine your map.

Q: Can concept maps be used for different levels of mathematics?

A: Yes, concept maps can be used effectively at all levels of mathematics, from elementary school to advanced university courses. The complexity of the map will vary depending on the level of the subject matter.

Q: Are there any software tools that can assist in creating concept maps?

A: Yes, several software tools are available for creating concept maps, including CmapTools, MindNode, and XMind. These tools offer features like pre-designed templates, automatic layout, and collaboration capabilities.

Tips for Effective Concept Mapping in Mathematics

• Use clear and concise labels for concepts and links.
• Employ different colors and shapes to distinguish different types of concepts.
• Keep the map visually appealing and easy to understand.
• Use a consistent format for your map, ensuring a clear hierarchical structure.
• Regularly review and revise your concept map to ensure its accuracy and completeness.

Conclusion

Concept mapping emerges as a powerful tool for unlocking mathematical understanding. By visually representing the interconnectedness of concepts, it enhances comprehension, improves memory recall, fosters critical thinking, and facilitates problem-solving. Whether employed by students, teachers, or researchers, concept maps provide a valuable framework for navigating the intricacies of mathematical knowledge and fostering a deeper appreciation for the beauty and logic of this fascinating discipline.

Closure

Thus, we hope this article has provided valuable insights into Unlocking Mathematical Understanding: A Comprehensive Guide to Concept Mapping. We appreciate your attention to our article. See you in our next article!