The Power Of Simplification: Unveiling The Logic Behind Karnaugh Maps And Sum-of-Products Expressions

The Power of Simplification: Unveiling the Logic Behind Karnaugh Maps and Sum-of-Products Expressions

Related Articles: The Power of Simplification: Unveiling the Logic Behind Karnaugh Maps and Sum-of-Products Expressions

Introduction

With great pleasure, we will explore the intriguing topic related to The Power of Simplification: Unveiling the Logic Behind Karnaugh Maps and Sum-of-Products Expressions. Let’s weave interesting information and offer fresh perspectives to the readers.

The Power of Simplification: Unveiling the Logic Behind Karnaugh Maps and Sum-of-Products Expressions

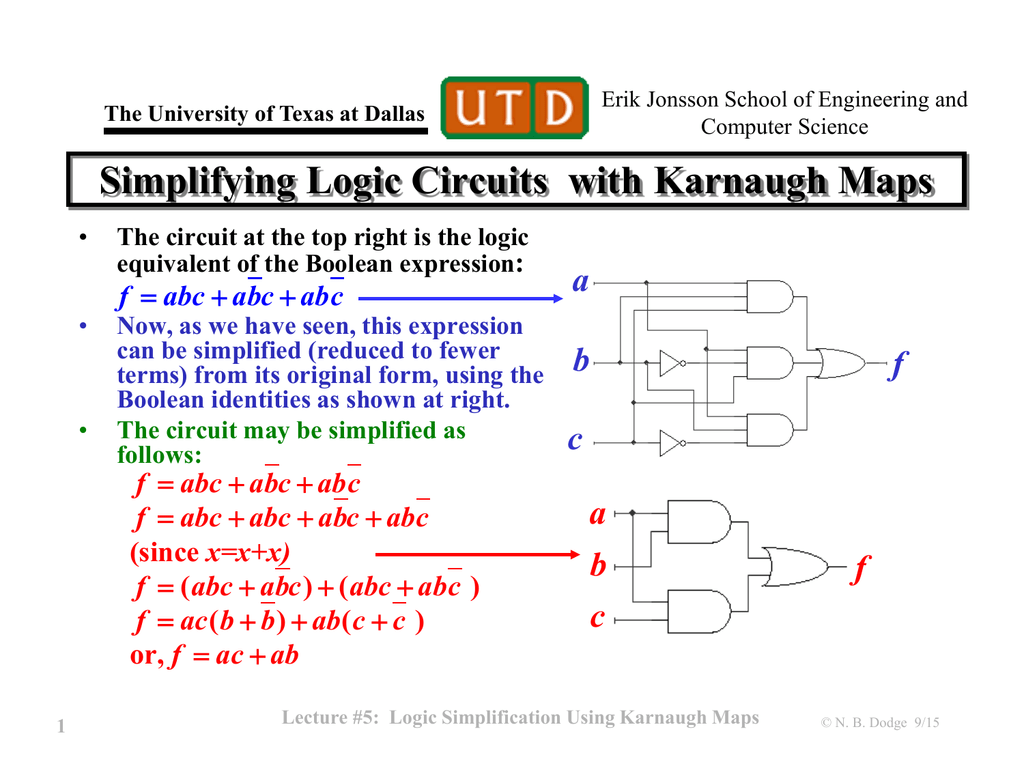
In the realm of digital logic design, where circuits are constructed from intricate combinations of gates, the need for efficient and streamlined solutions is paramount. Karnaugh maps, or K-maps, offer a powerful visual tool to simplify Boolean expressions, paving the way for optimized circuit designs. This article delves into the core principles of K-maps and their utilization in deriving simplified sum-of-products (SOP) expressions, highlighting the benefits and intricacies of this method.

Understanding Boolean Expressions and Logic Gates

Before embarking on the intricacies of K-maps, it is crucial to grasp the fundamental concepts of Boolean algebra and logic gates. Boolean algebra, named after the mathematician George Boole, provides a mathematical framework for representing and manipulating logical operations. Logic gates, the building blocks of digital circuits, perform specific logical operations on binary inputs (0 or 1) to produce a binary output.

Common logic gates include:

• AND Gate: Outputs a 1 only if all inputs are 1.
• OR Gate: Outputs a 1 if at least one input is 1.
• NOT Gate (Inverter): Inverts the input, outputting a 1 if the input is 0, and vice versa.

Boolean expressions, constructed using these logic gates and operators (AND, OR, NOT), represent the logical behavior of a circuit. These expressions can be complex and difficult to decipher, especially for circuits with numerous inputs.

Karnaugh Maps: A Visual Approach to Simplification

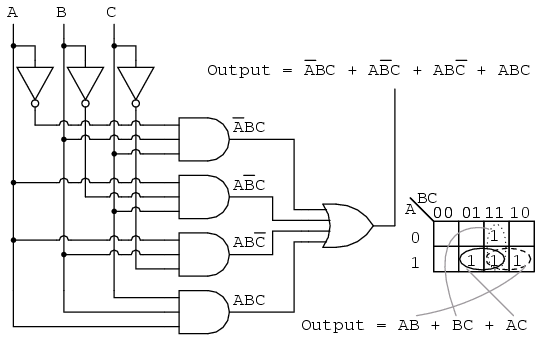
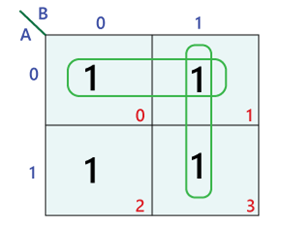
Karnaugh maps offer a visual representation of Boolean expressions, enabling the identification of redundant terms and simplification of the expression. They are essentially a graphical representation of a truth table, where each cell corresponds to a unique combination of input variables.

Constructing a K-map:

1. Determine the number of variables: The number of input variables dictates the size of the K-map. For example, a 2-variable K-map has 2^2 = 4 cells, while a 3-variable K-map has 2^3 = 8 cells.

2. Assign binary values to cells: Each cell in the K-map represents a unique combination of input variables, assigned according to a specific binary pattern. The order of variables and the arrangement of cells are crucial for effective simplification.

3. Populate cells with output values: For each combination of input variables, the corresponding output value from the truth table is placed in the appropriate cell.

Simplifying Boolean Expressions using K-maps:

The key to simplification lies in grouping adjacent cells containing ‘1’ values in the K-map. These groups represent terms that can be combined using the following principles:

• Adjacent cells: Cells sharing a common edge (horizontal or vertical) are considered adjacent.
• Grouping size: Groups should be as large as possible, with the size being a power of 2 (1, 2, 4, 8, etc.).
• Wrapping around: K-maps can wrap around, meaning that cells on opposite edges can be considered adjacent.

Deriving the Sum-of-Products Expression:

Once the groups are formed, the simplified SOP expression is obtained by:

1. Identifying the variables that remain constant within each group: For each group, note the variables that have the same value in all cells within the group.
2. Forming a product term for each group: For each group, form a product term by ANDing the variables that are constant within the group. If a variable is 0 in the group, its complement is included in the product term.
3. Combining product terms: The simplified SOP expression is formed by ORing the product terms obtained for each group.

Benefits of Using K-maps:

• Simplicity and Visualization: K-maps provide a visually intuitive approach to Boolean expression simplification, making it easier to identify redundant terms and optimize expressions.
• Efficiency: K-maps often lead to significantly simpler expressions compared to algebraic manipulation, reducing the complexity of the circuit design.
• Reduced Logic Gates: Simplifying Boolean expressions results in fewer logic gates required in the circuit, leading to lower cost, smaller size, and reduced power consumption.

Understanding the Sum-of-Products (SOP) Form

The sum-of-products (SOP) form is a standard way to represent Boolean expressions. It is a combination of product terms (AND operations) connected by OR operations. Each product term represents a specific combination of input variables that produce a high (1) output.

Example: Implementing a Full Adder using K-map and SOP

A full adder is a fundamental building block in digital circuits, capable of adding two binary bits along with a carry-in bit. Let’s illustrate the process of simplifying a full adder using K-map and SOP:

1. Truth Table: The truth table for a full adder defines the output (sum and carry-out) for all possible combinations of input bits (A, B, Carry-in).

2. K-map Construction: A 3-variable K-map is used to represent the sum and carry-out outputs.

3. Grouping and Simplification: Adjacent cells with ‘1’ values are grouped together.

4. SOP Expression: The simplified SOP expressions for sum and carry-out are derived from the groups in the K-map.

FAQs about K-maps and SOP:

Q1: What are the limitations of K-maps?

A: K-maps are effective for simplifying expressions with up to 5-6 variables. For expressions with more variables, the map becomes increasingly complex and difficult to manage.

Q2: Can K-maps be used for expressions with more than 4 variables?

A: Yes, but for expressions with more than 4 variables, multiple K-maps are used, with each map representing a subset of variables.

Q3: What are the alternative methods for Boolean expression simplification?

A: Other methods include algebraic manipulation, Quine-McCluskey algorithm, and Espresso heuristic logic minimizer.

Tips for Using K-maps:

• Start with a clear truth table: Ensure the truth table accurately represents the desired logic function.
• Use a systematic approach: Follow a consistent pattern when assigning binary values to cells and grouping adjacent cells.
• Double-check your work: Verify the simplified expression against the original truth table.

Conclusion:

Karnaugh maps and the sum-of-products form are powerful tools for simplifying Boolean expressions, leading to optimized circuit designs. By understanding the principles of K-maps and their application in deriving SOP expressions, digital logic designers can create efficient and cost-effective circuits for various applications. While K-maps have limitations for expressions with many variables, they remain an invaluable technique for simplifying logic functions, paving the way for streamlined and optimized digital systems.

Closure

Thus, we hope this article has provided valuable insights into The Power of Simplification: Unveiling the Logic Behind Karnaugh Maps and Sum-of-Products Expressions. We hope you find this article informative and beneficial. See you in our next article!